多重网格方法求解不可压流体

多重网格方法是效率很高的算法。

翻译自 A parallel multigrid Poisson solver for fluids simulation on large grids

1. 前言

略

我们主要的贡献

在自由表面流模拟中，混合了任意Dirichlet边界和Neumann边界的非规则体素化区域很常见，我们给出了处理这种问题的通用方法。之前有文章提出矩形区域上的几何多重网格方法[TO94, AF96, BWRB05, BWKS06, KH08]，也有文章提出非规则Neumann边界条件的处理(通过投影方法)[MCPN08]，但是没有将问题推广到一般情况。

我们使用了纯几何的、无矩阵的格式，并且收敛率能保持在常数的，与边界、几何无关。[BWRB05]提出了一种轻量的、无矩阵的几何多重网格方法应用于均匀的矩形区域的求解，然而将它推广到体素化区域很困难。[HMBVR05]在离散边界时嵌入了切割单元，导致体素化Poisson方程的离散不收敛，因为边界处出现了不稳定现象(啥不稳定?)。据[CLB09]所说，即使使用高阶嵌入也不能得到常数收敛率，他们在嵌入背景格子的表面网格上求解Poisson方程时，注意到当格子不能解析网格时，收敛率会退化。由于找到收敛的几何解很困难[CFL07,CGR04,PM04]，很多人选择使用更加通用的代数多重网格方法，但是代数多重网格方法的初始化很耗费资源，并行化困难[TOS01]。

相较于广泛使用的ICPCG(incomplete Cholesky preconditioned conjugate gradient)求解器，我们的方法占用的内存少，收敛效果更好，并且更容易并行化。不像ICPCG，我们的方法不用显式存储预处理矩阵，能够在16GB内存中处理 $768^2\times 1152$ 个体素。ICPCG需要稀疏回代过程(sparse backsubstition)，为了让这过程能够并行化，算法上需要做很多调整，而我们提出的方法不存在这个问题。最后，在中等规模的问题上，我们的求解器的速度相对于ICPCG有大幅提升，并且收敛率与网格大小无关，因此随着问题规模增加，我们的优势会更加明显。对于分辨率为 $128^3$ 的问题，我们可以在0.75秒内使残差下降 $10^4$ ，对于 $768^3$ 的问题则只需大约一分钟。

2. 相关工作

多重网格方法的效率非常高，它在图形学中的应用非常多，包括图像处理[KH08, BWKS06, RC03], 烟雾模拟[MCPN08]，网格变形[SYBF06], 薄壳模拟 [GTS02], 布料模拟 [ONW08], 流体模拟 [CFL∗07, CTG10], 几何处理 [NGH04], 固体形变模拟 [OGRG07], 渲染 [Sta95, HMBVR05], 并已有效地移植到GPU [BFGS03, GWL∗03, GSMY∗08]。该领域大量工作聚焦于矩形区域的求解或者结合代数多重网格方法在非规则区域的求解，我们给出一些涉及了非规则区域和几何多重网格的工作。[HMBVR05]和[CLB∗09]将非规则区域嵌入规则的格子中，给出了非规则模板(用于迭代的模板？)。[RC03, ONW08]使用了从粗到细的几何网格层次，保证了不同网格层之间的网格能够对齐，但是这些方法要求网格在粗网格层能够完全解析(细网格由粗网格决定)，因此这种方法无法解析精细的流体特征[SAB∗99]将多重网格作为CG方法的预处理器使用，而不是独立的求解器，这样能缓解一些算例中出现的不稳定现象。多重网格方法作为预处理器求解Poisson方程可以参考论文 [Tat93] 它的并行化可参考 [TO94] 以及 [AF96]。[KH08] 引入了高阶并行多重网格求解器处理大型矩形图像。

3. 方法概览

我们要求解的是Poisson方程，见式(1)。

\begin{gathered} \Delta p=f \text { in } \Omega \subset \mathbf{R}^3 \\ p(\mathbf{x})=\alpha(\mathbf{x}) \text { on } \Gamma_D, \quad p_n(\mathbf{x})=\beta(\mathbf{x}) \text { on } \Gamma_N \end{gathered} \tag{1}

区域边界 $\partial \Omega=\Gamma_D \cap \Gamma_N$ 被分成两个不相交的子集 $\Gamma_D$ 和 $\Gamma_N$ ，分别施加
Dirichlet边界条件和Neumann边界条件。对于流体模拟， $\Omega$ 对应物体或液体，Dirichlet边界条件施加在空气和水的界面上，Neumann边界条件施加在流体和浸没固体(或容器内壁)的边界。不失一般性，我们假设Neumann边界条件为零 $(\beta(\mathbf{x})=0)$ ，因为非零边界条件可以通过修改右端项实现。

注：这其实很好理解，速度为Dirichlet边界的时候，压强为Neumann边界。

3.1 离散

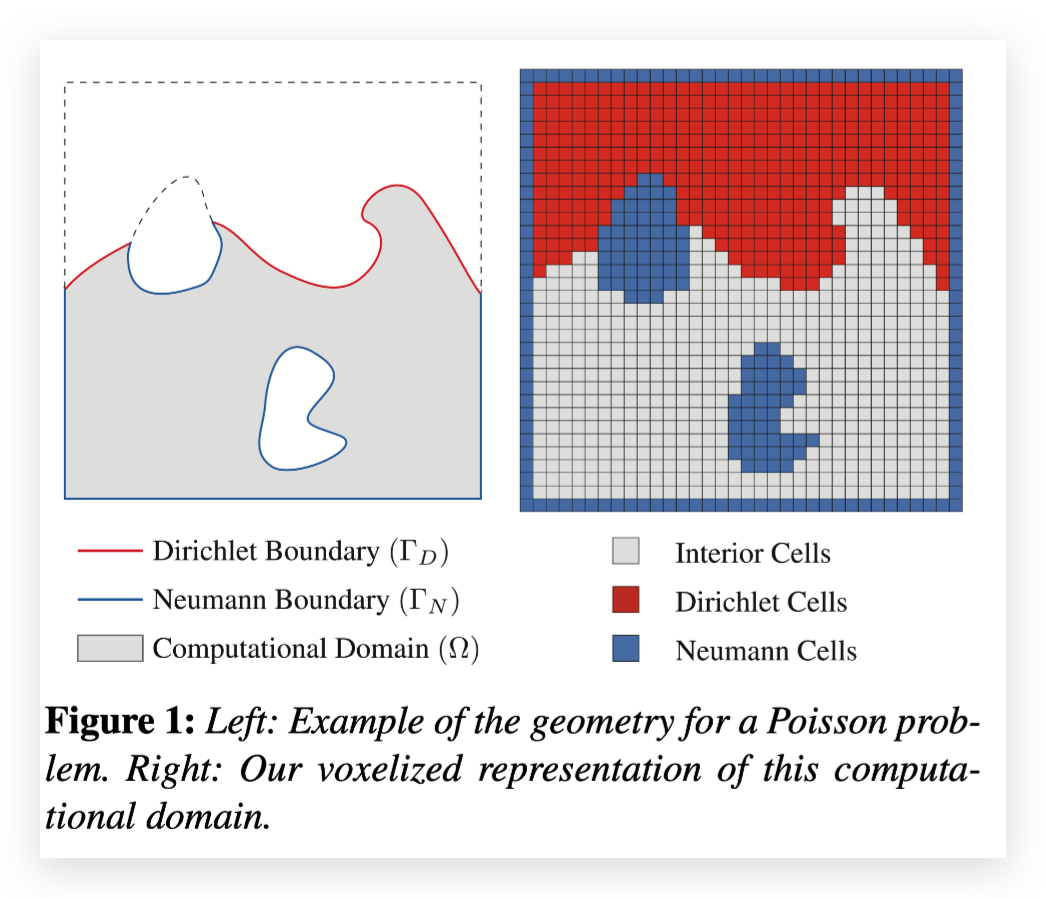
我们将Poisson方程在均匀的笛卡尔网格上离散，将未知的压强变量 $p_{ijk}$ 存储在单元格的中心。在我们的方法中，计算区域和边界区域的精度由背景网格决定。具体来说，计算区域以一系列网格单元(或体素)来表示，我们称它们是内部单元(图一右中的灰色单元)。我们将边界单元也体素化，将Dirichlet边界条件定义在一个体素化区域，而不是将它施加在边界 $\partial \Omega$ 上。我们称之为Dirichlet单元(图一右中的红色单元)。类似地，我们可以通过栅格化固体和容器内壁定义Neumann单元(图一右中的蓝色单元)。

因为压强定义在单元中心，Neumann边界条件可以很自然地施加在内部单元和Neumann单元的分界面上，我们在第四节中会给出简单实现。我们假设我们的计算区域周围一直都有Neumann单元作为“ghost”层，如图一所示。这样的假设不是一般性，因为对于Dirichlet边界，我们再加一层额外的Neumann单元也不影响 $\Omega$ 中的结果。对每一个内部单元，我们构造出如下Poisson方程的离散格式：

\begin{gathered} \sum_{\left(i^{\prime}, j^{\prime}, k^{\prime}\right) \in \mathcal{N}_{i j k}^*} \frac{p_{i^{\prime} j^{\prime} k^{\prime}}-p_{i j k}}{h^2}=f_{i j k} \\ \mathcal{N}_{i j k}=\{(i \pm 1, j, k),(i, j \pm 1, k),(i, j, k \pm 1)\} \\ \mathcal{N}_{i j k}^*=\left\{\left(i^{\prime}, j^{\prime}, k^{\prime}\right) \in \mathcal{N}_{i j k}: \operatorname{cell}\left(i^{\prime}, j^{\prime}, k^{\prime}\right) \text { is not Neumann }\right\} \end{gathered} \tag{2}

在这个定义中， $\mathcal{N}_{i j k}$ 表示和内部单元 $(i,j,k)$ 有共同表面的六个邻接单元的集合， $\mathcal{N}_{i j k}^*$ 是 $\mathcal{N}_{i j k}$ 的子集，排除了任意Neumann单元。 $h$ 表示网格步长。方程 (2) 是从标准的七点有限差分方法修改得到的，用零Neumann边界条件 $\left(p_{i^{\prime} j^{\prime} k^{\prime}}-p_{i j k}\right) / h=0$ 保证Neumann边界上的压强为零。在内部单元上，是标准的七点有限差分方法。这个公式和[FM96,FF01]中的公式是一样的。

3.2 多重网格迭代

我们介绍用几何多重网格方法求解式(2)定义的Poisson问题。我们的方法使用了V-Cycle作为多重网格校正格式[TOS01]，Algorithm 1给出了每一次V-Cycle迭代的伪代码。

V-Cycle 过程需要将Poisson在 $L+1$ 层网格上离散，将这些网格记为 $\mathcal{L}^{(0)}, \mathcal{L}^{(1)}, \ldots, \mathcal{L}^{(L)}$ ，其中 0 层网格是最细的网格，L层网格是最粗的网格。我们也定义了每一层网格的光滑子和不同网格层之间的限制/插值算子。

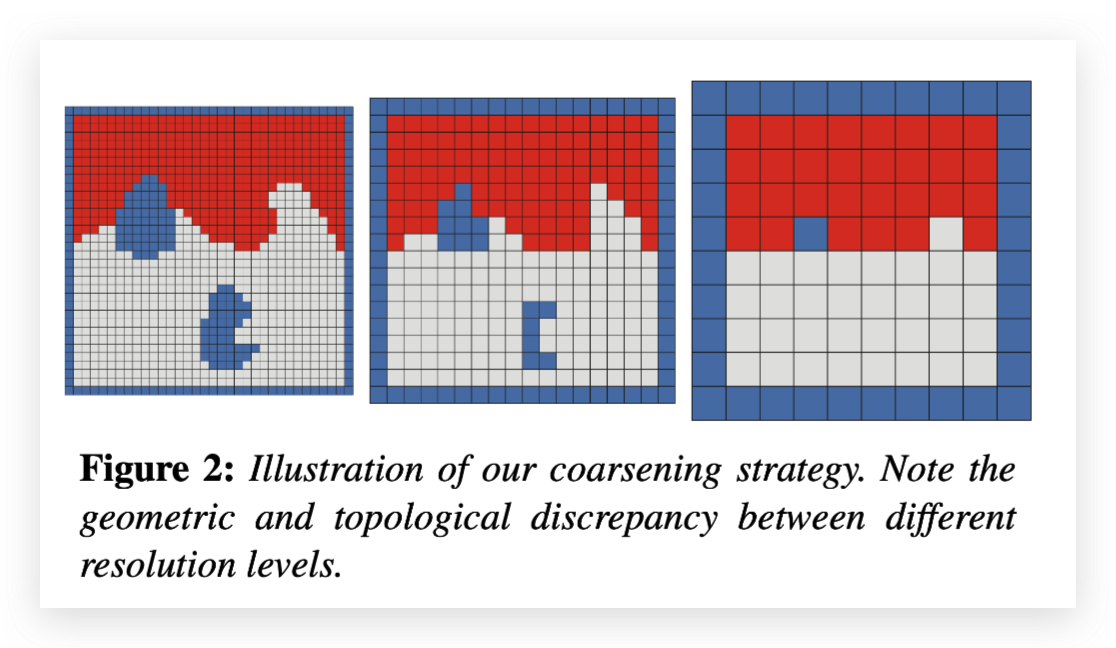
我们的方法是纯几何的，我们构造出每一层网格的像素化描述，将单元分类为内部单元、Dirichlet单元、Neumann单元。根据像素化表示构造出离散的Poisson算子 $\mathcal{L}$ 。每一层网格的粗化采用8-1的模板，生成网格间距为原网格两倍的粗网格。我们的层次结构很深：最粗的网格层通常是 $8 \times 8\times 8$ 。这样的粗化方法能够保证粗网格边界始终与细网格一致(见图2)。

如果一个粗网格单元粗化前的八个细网格单元中的任何一个是Dirichlet单元，那么它将被标记为Dirichlet单元。如果八个细网格单元中没有一个是Dirichlet单元，但至少有一个是内部单元，那么粗网格单元将被标记为内部单元。其他情况，则将粗网格单元标记为Neumann单元。

如图2所示，当粗网格不能精确解析细网格的特征时，这种粗化策略会导致细网格和粗网格之间存在显著差异，甚至会改变区域的拓扑结构，例如Neumann气泡会被吸收进内部区域，薄层状的内部区域会被吸收进Dirichlet区域。我们待会儿介绍这些差异会造成的影响。

definitions/背景格子

限制算子通过张量积木板构造， $\mathcal{R}=\mathcal{B} \otimes \mathcal{B} \otimes \mathcal{B}$ ，其中 $\mathcal{B}$ 是 $1 \mathrm{D}$ 模板，由4节点构成：

\begin{aligned} \left(\mathcal{B} \mathbf{u}^h\right)(x)=& \frac{1}{8} u^h\left(x-\frac{3 h}{2}\right)+\frac{3}{8} u^h\left(x-\frac{h}{2}\right)+\\ &+\frac{3}{8} u^h\left(x+\frac{h}{2}\right)+\frac{1}{8} u^h\left(x+\frac{3 h}{2}\right)=u^{2 h}(x) \end{aligned}

图三左给出了该张量积木板的2D形式，由16个节点构成。因为我们的变量位于单元格中心，因此粗网格上的变量和细网格上的变量不会有位置重合的。

延拓算子通过 $\mathcal{P}^I=8 \mathcal{B} \otimes \mathcal{B} \otimes \mathcal{B}$ 定义，换句话说，就是转置、缩放后的限制算子我们可以验证这个延拓算子是一个三线性插值算子。只有当限制算子或插值算子的输出结果位于内部单元上时，我们才使用它们。当限制算子或插值算子的输入不位于内部单元时，我们用零值代替。

我们使用系数为 $w=2/3$ 的加权Jacobi迭代，用它求解Poisson方程是稳定的，并且在并行效率上比Gauss-Seidel方法好。对于具有混合边界条件和不规则几何区域的问题，通常要在计算区域边界附近执行额外的迭代计算。我们将距离Dirichlet单元或Neumann单元三个单元以内的内部单元记为边界区域，如图三右的黑色阴影区域所示。总之，我们在边界区域进行一些额外的Gauss-Seidel迭代，在整个区域进行加权Jacobi迭代。具体来说，我们一开始会在边界区域进行数次Gauss-Seidel迭代，然后再在整个区域进行加权Jacobi迭代，最后再在边界进行额外的Gauss-Seidel迭代。